12.05-13.05 АЛГ

АЛГЕБРА         для 7а и 7б

Здравствуйте, ребята!

Тема занятия   "Подсчет вариантов с помощью графов".

1. Ребята, сегодня мы закрепляем последние  темы курса 7 класса по алгебре. Посмотрите внимательно видео уроки и сделайте конспекты в тетрадь ОГЭ, кто не сделал.
ПОВТОРИТЕ

https://www.youtube.com/watch?v=pFD9Zxoy1yo&list=PLBnDGoKqP7bavlUKISZHhORjow_zDXh-i&index=49

Подсчет вариантов с помощью графов.
ПОСМОТРИТЕ ТЕ, КТО ХОЧЕТ ЗНАТЬ БОЛЬШЕ

ОГЭ по ИНФОРМАТИКЕ 3 задание 9 класс ГРАФ ПОСТРОЕНИЕ

https://www.youtube.com/watch?v=RV-6BYv7R5k

2.Прочитать § 40 .

 3.Повторяем материал для подготовки к ВПР
https://www.youtube.com/watch?v=bPVSVUx5AE0

ВПР по математике 7 класс, 1 задание

Попробуйте решить и проверьте себя.

Задача.

У Ирины есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?

Решение. С помощью составленной ниже таблицы пар выпавших точек можно утверждать, что число всевозможных пар равно 6.

Ответ: 6.

4. ПОВТОРЯЕМ:

1. Основные положения теории графов

Граф состоит из двух множеств: конечного множества элементов – вершин, и конечного множества элементов – ребер. 

Геометрически граф – это структура, состоящая из разбросанных в пространстве точек (вершин), соединенных системой линий (ребер). 

При изображении графа не имеет значения расположение вершин на плоскости, кривизна и длина ребер. 

Геометрический граф является удобным представлением любых графов.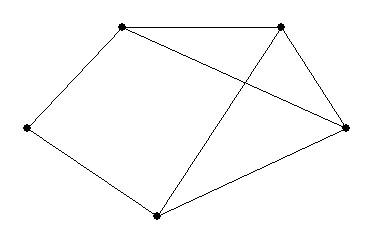

Граф, который можно начертить на плоскости таким образом, чтобы его ребра пересекались только в вершинах, называется плоским графом. 

Граф, на котором указано направление каждого его ребра, (что обычно показывается стрелкой) называется ориентированным графом.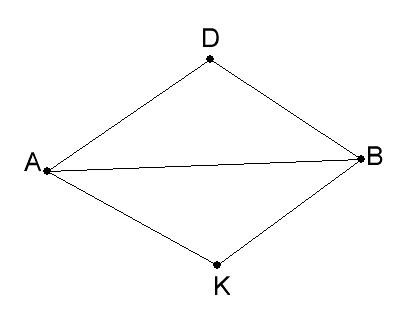

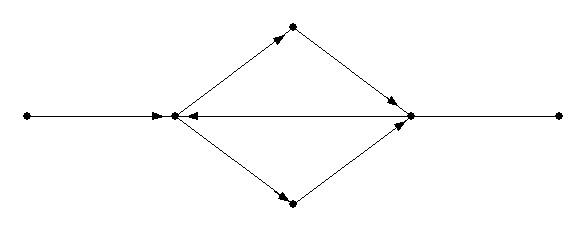
Линия на графе, быть может проходящая даже по нескольку раз через одни и те же вершины, не содержащая одних и тех же ребер, называется цепью.

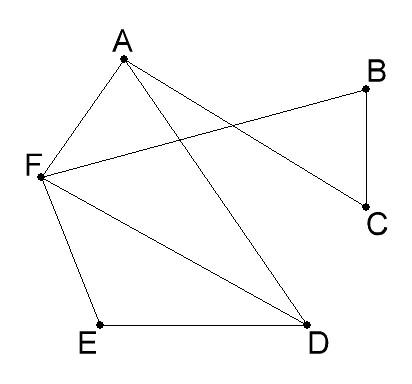
Замкнутая цепь, которая начинается и оканчивается в одной и той же вершине, называется циклом АFЕДFВСА.

Если каждую вершину графа можно соединить с любой другой его вершиной некоторой цепью, то граф называется связным. В теории графов предполагают, что рассматриваемые графы являются связными.

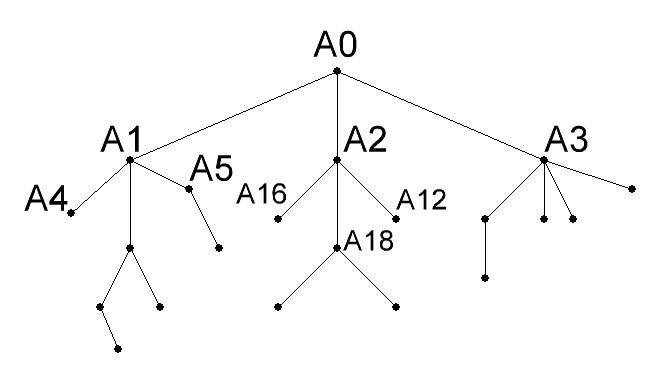
Деревом называется связной граф, не содержащий циклов. Такой граф не имеет кратных ребер. Для каждой пары его вершин существует единственная соединяющая их цепь.

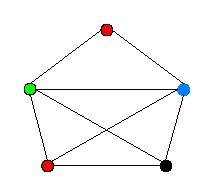
2. Решение задач с помощью графов

Будем считать, что граф – это совокупность объектов со связями между ними. Объекты (элементы множества) представим как вершины, а связи между ними как ребра. Для удобства иллюстрации условия задачи, вершины графа заменим кругами или прямоугольниками там, где это целесообразно.

1. Команда космического корабля должна состоять из командира, пилота и врача. На пост командира претендуют 3 кандидата: К1, К2, К3; на пост пилота тоже 3 кандидата: Р1, Р2, Р3; а на пост врача 2 кандидата: В1, В2. При изучении психологической совместимости членов экипажа выяснилось, что:

– К1 несовместим с Р2 и В1; – Р2 несовместим с В2;

– К2 несовместим с Р3; – Р3 несовместим с В1.

– К3 несовместим с Р3 и В2;

Сколько вариантов экипажей возможно сформировать?

Решение

Для решения данной задачи построим граф-дерево, вершинами которого являются члены экипажа, а ребрами выражена совместимость членов экипажей.

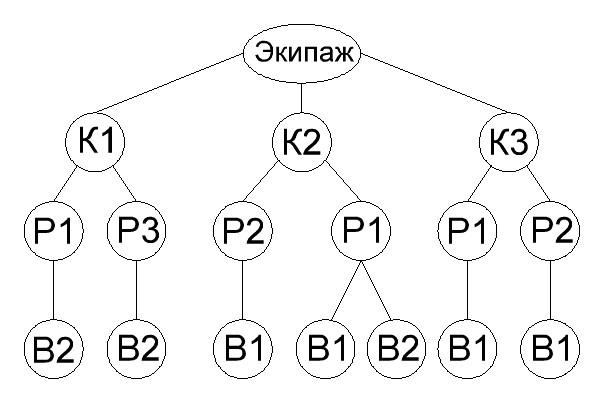
Ответ: 7 вариантов.

3. Марина, Лариса, Жанна и Катя умеют играть на разных инструментах (пианино, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один. Известно:

1. Девушка, которая играет на гитаре, говорит по-испански.

2. Лариса не играет ни на скрипке, ни на виолончели и не знает английского.

3. Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского.

4. Девушка, которая говорит по-немецки, не играет на виолончели.

5. Жанна знает французский язык, но не играет на скрипке.

Кто на каком инструменте играет, и какой иностранный язык знает?

Решение

Построим граф, вершинами которого являются имена девочек, названия языков и инструментов, а ребрами – информация о девочках. По условию задачи между элементами множеств существует взаимно-однозначное соответствие. Вершины, соответствующие именам девочек, соединяем с вершинами, соответствующими названиям языков или инструментов сплошными направленными отрезками-ребрами, если девочки ими владеют, в противном случае – пунктирными. Так «Ж» соединим с «Ф» (условие 5), а «Г» можем соединить с «И»(условие 1) сплошными ребрами. «Л» соединяем с «С», «В», «А» (условие 2); «М» соединяем с «С», «В», «Н» и «А» ( условие 3); «Н» с «В» ( условие 4); «Ж» с «С» (условие 5) пунктирными ребрами.

На построенном графе видно, что Марина знает испанский язык и играет на гитаре. Лариса знает немецкий язык, значит, Катя владеет английским. Лариса играет на пианино, Жанна – на виолончели, значит, Катя играет на скрипке.

Ответ: Марина знает испанский и играет на гитаре, Лариса знает немецкий и играет на пианино, Жанна знает французский и играет на виолончели, Катя знает английский и играет на скрипке.

5. Только что приобретенные вами знания имеют порой любопытное применение. Великий математик Л. Эйлер в 1736 г. занимался решением такой своеоб­разной задачи:  В Кенигсберге река, омывающая два острова, де­лится на два рукава, через которые перекинуто семь мостов (рис. 23). Можно ли обойти все эти мосты, не побывав ни на одном из них более раза?

Схема мостов Кёнигсберга

     рис. 23

6. Алгоритм решения задач при помощи графов

- проанализировать условие задачи;

- определить, что известно;

- составить граф:

- проанализировать граф, найти все возможные решения или доказать, что их нет.

7.  Домашнее задание. 

1)  Учебник : читать § 40 ответить письменно на вопросы стр. 268;

2) № 715; Попробуйте решить задачу 5.

3)  Сделать КРАТКО конспекты видео уроков в тетрадь ОГЭ. Не забудьте сделать проверочную работу в Яклассе!